Measure theory  

• Line of thoughts
  • Given a set X, define a sigma-algebra (also called sigma-field or sigma-ring) \cal{F}, which satisfies the following three properties:
    • empty set \phi and X are in \cal{F}
    • closed under countable union
    • closed under complement
  • Define a measure \mu on this sigma-algebra; all elements in the sigma-algebra are \mu-measurable set.   A measure satisfies the following three properties
    • 0<= \mu(A)<= \infty, for all A in \cal{F}
    • \mu(\phi) = 0
    • \mu is countably additive (sigma-additive)
  • Define a measurable function 
    • A function f is measurable on X if all its level sets are measurable. A level set is {x: f(x)<c}, where inf(f(x))<=c<=sup(f(x)), x \in X.
  • Define an integrable function 
    • A function f is integrable on X if 1) it can be represented almost everywhere by the limit of a sequence of simple functions \psi_n(x) which converges almost everywhere on X; and 2) the integral of \psi_n(x) on X is bounded for all n. ?
  • Define the integral of an integrable function
    • The integral of an integrable function is the limit of the sequence of integrals of \psi_n(x) on X.
  • Define function spaces in terms of Lebesgue integral: 
    • L^p(E) (p>1 is a real number): 
      • f is in L^p(E) if f^p is integrable on the set E and the integral of f^p is finite.
      • special cases: L^1(E), L^2(E)
    • L^{\infty}(E)
      • f is in L^{\infty}(E) if the essential supremum of f is finite.  
      • Only on a set of measure zero, f takes values greater than the essential supremum.
      • L^{\infty}(E) is a vector space over the field R.
  • Define sequence spaces: (integral is replaced by infinite summation)
    • l^p(n), l^p, l^{\infty} 
  • Define Hilbert space (inner-product space) 
    • It is a complete space with inner product defined.  That is, it is a Banach space with inner product defined.
    • Special properties of Hilbert space
      • Parallelogram identity (natural generalization of Euclidean geometry, parallel postulate)
      • Define a generalized Fourier series with any complete orthonormal set.  
        • Every function in a separable Hilbert space has a unique generalized Fourier-series representation w.r.t. the corresponding orthonormal set.
      • If the basis is an orthonormal set but not complete, use Bessel's inequality instead of Parseval's formula.
      • A Hilbert space H is separable if and only if there is a complete orthonormal set in H.
  • Normed space, metric space, Hilbert space, measure space
    • Normed space and Hilbert space have a significant overlap.     
      • We can use inner product to define a norm by ||x|| = <x,x>. But some norm cannot be defined by an inner product. For example, L^{\infty} norm cannot be defined by an inner product.
      • Jordan-Von Neumann theorem, stating a necessary and sufficient condition for a normed vector space to be a inner product space: the keys are parallelogram law and polarization identity.
    • A metric space can be induced by a normed space via d(x,y)=||x-y||.
    • Metric space and Hilbert space have a significant overlap. 
      • We can use inner product to define a norm by ||x|| = <x,x>. Then define d(x,y)=||x-y||=<x-y,x-y>. But L^{\infty} norm cannot be defined by an inner product. 
    • Measure space is defined by a triplet (X, sigma-algebra F, measure m).
      • Completeness of a measure space
        • (Definition) If A \in F and if B is a subset of X with m(A\B)+m(B\A)=0, then B \in F.
        • Note this is different from the completeness of a normed space (every Cauchy sequence converges).

• Separabililty of a metric space
  • A metric space is said to be separable if it possesses a dense subset consisting a countable number of elements.  ("dense subset" will be defined later.) 
• Metric spaces:
  • If m(E)<\infty and 0<q<p, then L^p(E) is a subset of L^q(E).   E.g., L^1(E) \supset L^2(E) \supset L^3(E) ....
  • The negation of the preceding proposition (if m(E)=\infty) is not true.
• Measurable space: 
  • (X, \cal{F}) is a measurable space if 
    1. \cal{F} is a sigma-field defined on X, and 
    2. a measure can be defined on \cal{F}.
  • If \cal{F} is a sigma-field and a measure can be defined on \cal{F}, we can say (X, \cal{F}) is a measurable space without explicitly defining a measure.  For example, a Borel field is measurable.
• Measure space:
  • If a measure \mu is defined on a measurable space (X, \cal{F}) , then  (X, \cal{F},\mu) is called a measure space.

• Line of thoughts (Probability measure)
  • For a given set X, first define algebra B (closed under finite set-theoretic arithmetic)
  • Then define sigma-algebra F (closed under countable set-theoretic arithmetic);
    • For an arbitrary collection B of subsets of X, we can always use a method (see textbooks) to generate smallest sigma-algebra containing B.   Denote it by \sigma(B).
    • Typically we start with Borel algebra and obtain Borel sigma-algebra.  The nice thing about Borel sets are that intervals have well-defined measure (length).
  • Then define a probability measure m on an algebra B, which satisfies three properties (this is always possible since we can start with Borel algebra and the measure is simple length of interval).
    • Nonnegativity
    • m(empty set) =0; m(X)=1
    • countable additivity
  • The measure m defined on algebra B is too restrictive.   There are many subsets of X, to which the measure m is not applicable.  Then we extend the measure m to a larger class, which is a sigma-algebra. 
    • We first define an outer measure m* based on the measure m, for the power set.   This is easy.   For any subset A, we can always find a collection of elements (open intervals) b_i in B to cover A.  Then, define m*(A)=inf {\sum m(b_i)}.
    • Then define inner measure m_*(A)= 1 - m*(complement of A).
    • If m*(A)=m_*(A), we define P(A)=m*(A).   All subsets of X that have measure in this new definition, form a collection denoted by M (proven to be a sigma-algebra and contain \sigma(B)). 
    • Nice things of the new measure space (X, M, P) are that
      • P is countable additive (P is proven to be a measure!  Different from m which is from natural concept of length.)
      • (X, M, P) is complete.  That is, that a set C is a subset of D, D \in M, and P(D)=0, implies that C \in M and hence P(C)=0.  (X,B,m) is not complete!
      • Every element in M is measurable.   Note that M contains much more elements than B.
    • Probability measure is a Lebesgue measure with P(X)=1.  (Lebesgue measure in a general sense can set m(X) to be any positive number including infinity.)
• sigma means countable.  E.g., sigma-algebra is closed under countable unions; sigma-additivity of a measure means additivity for countable unions of disjoint sets.

Basics of Set Theory and General Topology

• Classification of points
  • Interior point of a set S:
    • A point x is called interior point of S if there exists a neighborhood of x completely contained in S. The set of all interior points of S is called the interior, denoted by int(S). 
    • (Another definition) A point x is an interior point of a set S if there exists a $\delta$ such that if ||y-x||<\delta, then y is in S.
  • Boundary point of S: a boundary point does not have to be in S.
    • A point x is called boundary point of S if every non-empty neighborhood of x intersects S and the complement of S. The set of all boundary points of S is called the boundary of S, denoted by bd(S). 
    • (Another definition) For every r>0, the neighborhood of x, N(x,r) contains a point p that is different from x and is not in S.
    • Interior point and boundary point are opposite concepts.  A point cannot be both interior and boundary point of S.
  • Accumulation point of S (also called cluster point or limit point) 
    • Three definitions:
      • A point x is said to be a limit point of S if every open set containing x contains a point of S distinct from x.
      • For every r>0, the neighborhood of x, N(x,r) contains a point of S distinct from x.
      • A point x is called accumulation point, if every neighborhood of x contains infinitely many distinct points of S. 
    • An accumulation point could be either an interior point or boundary point of S.
    • An accumulation point does not have to be in S.  For example, c is an accumulation point of the interval (c, d) but c is not in (c,d).
  • Isolated point x of S
    • There exists a neighborhood of x such that the intersection of the neighborhood and S is {x}; that is, the neighborhood does not contain any point of S except x.
    • Accumulation point and isolated point are opposite concepts.
    • The set of all integers only has isolated points but does not have accumulation points.  The set of all rational numbers only has accumulation points but does not have isolated points.
• Bounded set
  • A set S is said to be bounded above if there exists a number b such that x<= b for every x in S.
  • A set S is said to be bounded below if there exists a number b such that x>= b for every x in S.
  • The least upper bound (supremum) of S is an upper bound that is less than or equal to any other upper bound. Denote it by sup S.
  • The greatest lower bound (infimum) of S is a lower bound that is greater than or equal to any other lower bound. Denote it by inf S.
  • A bounded set S may not contain sup S or inf S.
• Open sets and closed sets
  • A set is called open if it contains only interior points.   
  • A set is called closed if its complement is open.
    • A set is closed if and only if it contains all its limit points.   
    • A misconception: a set is closed if it is not open.
  • Some sets are both open and closed, e.g., empty set and the whole set.   Some sets are neither open nor closed, e.g., (a,b].
  • Why open sets are so important?   They are used to Borel sets, compact sets.  A topology must be a collection of open sets if a metric is defined.   Note that we first define topology, then define define metric space based on a topological space.
• Compact sets
  • For the real numbers:
    • A set S of real numbers is called compact if every sequence in S has a subsequence that converges to
      an element contained in S. 
  • The above definition of compact sets using sequence can not be used in more abstract situations. We would also like a characterization
    of compact sets based entirely on open sets. We need some definitions first. 
  • Open Cover
    
    Let S be a set of real numbers. An open cover of S is a collection C of open sets such that S is contained by the union of the sets in C.
    The collection C of open sets is said to cover the set S. 
    
    A subset of sets from the collection C that still covers the set S is called a subcovering of S. 
  • Definition: A set S of real numbers is compact if and only if every open cover C of S can be reduced to a finite subcovering. 
  • Heine-Borel Theorem:  
    • A set is compact if and only if it is closed and bounded.
  • Bolzano-Weierstrass Theorem: 
    • Every bounded infinite set has an accumulation point.
    • Bolzano-Weierstrass Theorem is equivalent to Heine-Borel Theorem.
  • Nested sets are a sequence of sets A_n  that are decreasing: every 'next' set A_{n+1} is a subset of its predecessor A_n.
  • Intersection of nested compact sets are not empty.
  • Why define compactness of a set?  Nice things about a compact set:
    • A compact set is closed and bounded.   A closed set contains all its accumulation points.  
    • A compact set S must have both its supremum and infimum in S.
    • If F is a closed set contained in a compact set, then F is also compact.
    • Every Cauchy sequence of a compact set S converges in S.  (completeness?)
    • If a function f is continuous on a compact set K, then f is uniformly continuous on K.
      • Then we can interchange the order of limit and integral. (?)
    • If a function f is continuous, then the image of a compact set under f is also compact.
    • If f is a continuous function on a compact set K, then f has its supremum and infimum attained on K.   In particular, f must be bounded on the compact set K.
    • If f is lower semi-continuous function on a compact set K, then f has its infimum attained on K.
• Closure
  • The closure of a set S is the intersection of all closed sets containing S.   The closure of S is the greatest lower bound of all closed sets containing S. 
  • S is equal to its closure if and only if S is closed.
• A subset B of A is called dense in A if every point of A is an accumulation point of B.
  • The set of all rational numbers Q is dense in R.
• The collection of all measurable sets on [a,b] is a sigma-algebra.  But a sigma-algebra may have nonmeasurable sets.  For example, the power set of [a,b] is a sigma-algebra but it has nonmeasurable sets.  Borel sigma-algebra is a sigma-algebra generated by the family of all intervals in [a,b] (or in R).  Borel sigma-algebra is a proper subset of the sigma-algebra, which is the collection of all measurable sets on [a,b].  So we have three levels (proper containing relations):
  • Borel sigma-algebra (every Borel set is measurable), whose cardinality is the cardinality of R.
  • The sigma-algebra, which is the collection of all measurable sets on [a,b]
  • The power set of [a,b] (it has nonmeasurable sets)
• Dependencies between topological spaces
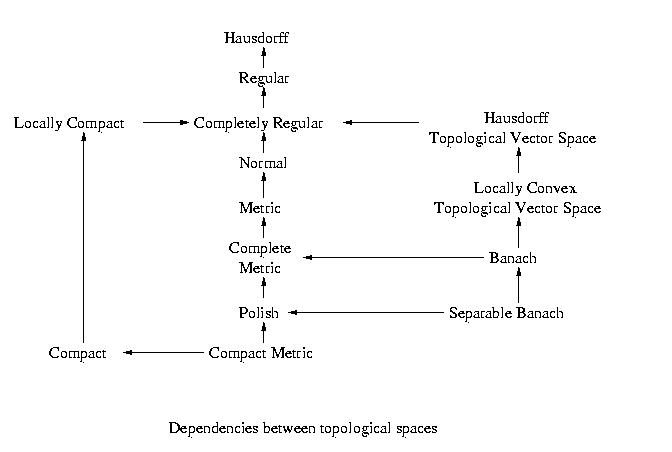
• Separation axioms: T_0 space to T_5 space
• Algebraic topology