Ideal codes for CDMA should have delta function as their autocorrelation functions, and 0 for cross-correlation functions, i.e.,
Walsh-Hadamard codes have large cross-correlation; they also have large autocorrelation for \tau \neq 0.
The autocorrelation function of m-sequence is close to \delta(\tau) and is robust to time offset. However, the cross-correlation of two m-sequences tends to be large.
Gold codes and Kasami codes, if carefully selected, have autocorrelation functions and cross-correlation functions close to the ideal codes. By "carefully selected", we mean we only choose those Gold codes and Kasami codes that have autocorrelation functions and cross-correlation functions close to the ideal codes. In other words, some Gold codes and Kasami codes have large cross-correlation; and/or they have large autocorrelation for \tau \neq 0.
The spreading of the data signal in a cdma system is done by applying a code, independent of the data-signal. Code-selection has a large impact on the performance of the system. On the one hand the longer the code, the higher the processing gain which enables us to allow more users in the system. On the other hand a larger processing gain implies the usage of more bandwidth. Another important property of the codes is the cross-correlation. If the codes which are used are not completely orthogonal, the cross-correlation factor is unequal to zero. In this situation the different users are interferers to each other, hence the near-far problem appears.
During the ber-analysis in the previous section the usual approach to assume pn-codesto be random [Roe77] was applied. In practical situations however, this assumption needs to be considered more carefully. This section proposes a strategy to select codes that are ```close to random''.
wissce is a hybrid DS/FH-system where both a code for direct-sequence spreading (a pn-code) and a code for frequency-hopping spreading (an fh-sequence) has to be selected. First the selection of pn-codes will be discussed.
A pn-codeused for DS-spreading consists of
units, called chips. These chips can have 2 values: -1/1 (polar) or 0/1. In the
following polar bit-sequences are used unless stated otherwise. As every data
symbol is combined with a single complete pn-code, the DS processing gain
is equal to the code-length. To be usable for direct-sequence spreading, a
pn-code must meet the following constraints:
Codes that can be found in practical DS-systems are: Walsh-Hadamard codes, m-sequences, Gold-codes and Kasami-codes. Walsh sequences [Bea75] are orthogonal while the other sequences show cross-correlation values unequal to zero [Gol67, Roe77, SP80].
Walsh-sequences have the advantage to be orthogonal, in this way we should get rid of any multi-access interference. There are however a number of drawbacks:
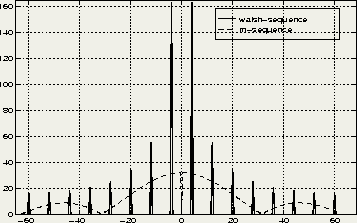
Figure 6.6: Frequency-domain comparison of a Walsh and an m-sequence
These drawbacks make Walsh-sequences not suitable for a system like wissce. Systems in which Walsh-sequences are applied are for instance multi-carrier cdma [YLF94] and the cellular cdma system IS-95 [Qua92]. Both systems are based on a cellular concept in which all users (and so all interferers) are synchronized with each other.
are not orthogonal, but they do have a narrow autocorrelation peak. The name
already implies that the codes can be created using a shift-register with
feedback-taps. By using a single shift-register, maximum length sequences (m-sequences)
can be obtained. Such sequences can be created by applying a single
shift-register with a number of specially selected feedback-taps. If the
shift-register size is n then the length of the code is equal to
. The number of possible codes is dependent on the number of possible sets of
feedback-taps that produce an m-sequence. These sequences have a number
of special properties. Some of them that will be considered in the code
selection process are mentioned here.
-envelope. In figure
6.6
the spectra of a Walsh-sequence of length 64 and an m-sequenceof length
63 are shown, both sequences contain (almost) the same power. The figure shows
that applying an m-sequence better distributes the power over the whole
available frequency range. here T denotes a delay of one chip and u is an m-sequence. By combining two shifts of this sequence (relative shifts i and j) the same m-sequenceis obtained, yet with another relative shift.
where k is an integer value, and
is the relative shift as a multiple of a chip-period.
and
. There do not exist preferred pairs for shift-registers with a length equal
to
where k is an integer. The product of two m-sequences which form a ``preferred pair'' leads
to a so-called Gold-code. By giving one of the codes a
delay with respect to the other code, we can get different sequences. The number
of sequences that are available is
(the two m-sequences alone, and a combination with
different shift positions). The maximum full-code cross-correlation has a value
of
.
In wissce the pn-code-length is chosen to be 63 (see section 5.2.3), consequently n=6. For this situation there are 65 different Gold-codes available and the maximum full-code cross-correlation is 17.
If a Gold-code is combined with a decimated version of one of the 2 m-sequences that form this Gold-code a ``Kasami-code from the large set'' is obtained. Such a code can then be formulated as follows:
where u and v form a preferred pair of m-sequences of
length
(n even). w is an m-sequenceresulting after decimation the v-code
with a value
. k is the offset of the v-code with respect to the u-code
and m is the offset of the w-code with respect to the u-code.
Offsets are relative to the state in which all register elements contain a one
or a minus one (all-ones state). In the large set of Kasami-codes a number of
special subsets can be observed:
Kasami-codes have the same correlation properties as Gold-codes. The
difference is the number of codes that can be created. For the large set of
Kasami-codes this number is equal to
. Choosing n equal to 6 as in
wissce gives 520 possible codes. As the number of codes determines the
number of different code addresses that can be created, the large set of
Kasami-codes is used as a code-set in
wissce. A large code-set also enables us to select those codes which
show good cross-correlation characteristics.
In
wissce the DS code-length (
) is chosen to be 63, this implies using shift-registers of length 6. Two codes
that form a preferred pair are: M(6,1) (feedbacks from the
and
feedback taps) and M(6,5,2,1). In the following we will use the notation
of (6.36).
Here n is even and equal to the length of the shift-registers used to
create u and v, u is the m-sequence with feedbacks
(6,1) and v is the m-sequencewith feedbacks (6,5,2,1). When
decimating M(6,1) sequence w is obtained, w is also an m-sequence:
M(3,2). The otherwise meaningless values for k and m are
used to denote special subsets.
Before starting the selection process, first the size of the code-set will be reduced by adding the constraint that the codes must be balanced to avoid a DC-offset. The initial code-set size now reduces from 520 to 241. The 241 balanced codes are used as a candidate set to the further code selection process. Having chosen a candidate code-set, we have to find a sub-set of this code-family which has good cross-correlation properties. As mentioned before partial sequence correlation is more important than full-sequence correlation. The reason for this is that all users in the system are asynchronous so the sequences will only overlap partially.
We saw that the multiple-access interference in a
cdma-system depends on the
-factor of two sequences k and i (equation
6.13
on page
).
So this parameter can be used as a criterion to select a code-set. The required
computational power however, to find a code-set with a bounded value of the
-factor among all codes in that set, goes exponentially with the size of the
initial candidate code-set. For a code-set size of 241 the calculation of a
code-set with bounded
-factor is therefore infeasible. Instead an algorithm as described in [EKB87]
will be used. Following this concept the codes are ordered in increasing value
of a cost-function. Assigning codes starts at the top of this list. In this way
the code-set is used which is likely to have the best correlation properties.
The cost-function is defined as:
where
is equal to the size of the code-set (in this case 241). The resulting sequence
of codes can be found in appendix
A.
Kasami code sequences can be implemented by multiplication of the outputs of 3 shift-registers (u, v and w) with proper feedbacks. Two shift-registers have length n (in wissce equal to 6) and form a ``preferred pair'', while the third sequence (w) resulted from decimation of the first sequence (u). The last shift-register has a length of 3. All three shift-registers create m-sequences.
To obtain all possible Kasami-codes, the 3 m-sequences should have different relative shifts with respect to each other. Two ``shift values'' play a role: the relative shift of the v-sequence and of the w-sequence, see (6.36).
As a relative shift of for instance 35 is costly to implement (we would need 35-6=29 extra delay-elements), the ``shift-and-add'' property can be applied (see (6.35)) to obtain the desired relative shift. It appears that all relative shifts can be created by using only 6 respectively 3 delayed versions of the v and w code. This is illustrated in figure 6.7, an additional requirement is that the sequences have their all-zero state at the same shift. In the figure the shift-parameters are referred to as m' and k' as there is a translation step between the relative shift values and the tap-numbers that are required to obtain those shifts. A description of the translation step can be also found in appendix A.
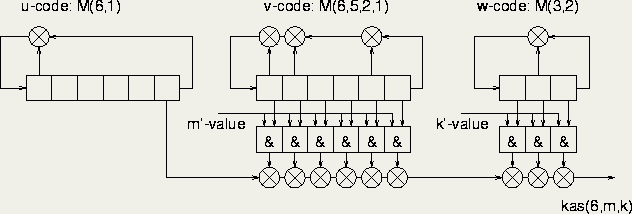
Figure 6.7: Kasami-code generator scheme
The code-selection process can be summarized in the following way:
In
wissce fh-spreading is applied to reduce the problems due to the
Near-Far effect. To keep the necessary bandwidth within
limits and the frequency synthesizers realizable, the
fh-sequence-length (
) is chosen equal to 7. For this rather short code-length it is possible to
perform a manual extensive search to find possible sequences. As a boundary
condition to the sequences we specified that a near-interferer should maximally
have 2 hits during a single fh-sequence. A possible code-set existing of
6 sequences is given in table
6.1.
A more general rule can be found in [MT92]. Hyperbolic codes which have the above mentioned property can be formed in the following way: if p is a prime, and there are p frequency-hop channels there exist p-1 codes of length p-1 which have in case of an asynchronous interferer at most 2 hits during a complete fh-sequence. We choose the first alternative because that provides longer sequences.
is the probability that a number of interfering users
are transmitting in the same frequency-hop channel as the reference user. This
probability will be referred to as
, where K is the total number of active users. This probability is
dependent on a number of system characteristics like:
As there are
fh-channels, the chance that two users ``hit'' is 1/
. The fh-sequences are selected on their property to have at most two
partial hits which leads to the following hit-probability [Gla92]:
This formula is only valid if random hopping is applied which is true as aa user can start transmitting at any arbitrarily moment.
The chance that 2 users have the same fh-sequenceis:
Two situations can be distinguished:
. We obtain for the complete hit probability:
However, the probability of interest is the chance that a certain number (k) of interfering users are present in the same frequency-hop channel as the intended user. This probability is given by:
where K is the total number of active users to be considered. In
figure 6.8
the expectation of (6.41)
is shown as a function of K. In this example
is equal to 7. The values from this plot can be used in formula (6.17)
on page
.
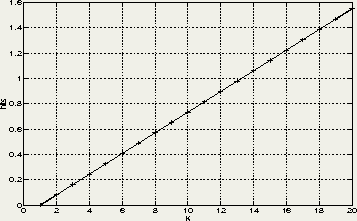
Figure 6.8:
as a function of K active users
From the figure above it is clear that even when quite a number of near-users is present, the ``mean'' value of the number of hits is limited to reasonable values. The wissce receiver should be able to operate under situations where more than 2 fh-channels are blocked. From the figure it appears that even if there are 20 near users, the mean number of hits is about 1.5.
|
A Larger Subset of Pseudo-Orthogonal Spreading Codes for WCDMA
João da Silva Pereira, Instituto Politécnico
de Leiria, Portugal |
Gold-sequences have been studied extensively and have found numerous applications in wireless communication systems. One example of this success is the third generation Universal Mobile Telecommunication System (UMTS), which should use segments of some sets of Gold-sequences as scrambling codes. This paper presents a new method to generate four times more PN-sequences that maintain the maximum peak cross-correlation at a low level. The cross-correlation improvement is more significant with longer sequences than with shorter sequences. A new set P(y,x) of PN-sequences is generated and may be used, for example, to increase the sets of Scrambling codes for UMTS.
Gold-sequences
are used mainly in modern communication systems with Spread Spectrum Code
Division Multiple Access (SS-CDMA). These applications often require large sets
of codes with highly peaked auto-correlation and minimum cross-correlation. The
principal features of these sequences are the ratio between the peak
auto-correlation value and the peak cross-correlation value, as well as the
average value of this ratio. In a noisy communication channel with multiple
users, these parameters are fundamental for the correct bit information
detection.
Among a large range of different families of binary and non-binary PN-sequences
,
the more classical one is the set of Gold-sequences. The purpose of this paper
is to analyze only the set of Gold-sequences that derive from m-sequences.
The objective is to be able to construct more PN-sequences using the same
circuit generator of Gold-sequences with minimum changes. However, the problem
of designing families of sequences having low values of the periodic and
aperiodic cross-correlation functions is a difficult one.
The new design is based in the same Gold-sequences generated in reverse mode. If all Gold-sequences are generated in reverse mode, than these sequences have the same peaks of periodic and aperiodic cross-correlation, and the periodic and aperiodic auto-correlations are still the same as for the original set of Gold sequences. Assembling these two sets, and calculating the new peak of periodic and aperiodic cross-correlation, it is possible to observe a small increase of these values. However, this increase seems to be not significant when the Gold-sequences are long.
More new sequences can be generated by mixing two sequences of the Gold set with a logical exclusive-or operation, when at least one of them is in reverse mode. The result is to increase four times the quantity of PN-sequences, keeping an acceptable level of cross-correlation.
You can represent the Gold set
by:
This is equivalent to:
The y and x are binary m-sequences of Nc bits constructed by means of two polynomial generators of degree n.
The y sequence is combined by a logical exclusive-or operation with each row of the X matrix, which is a set of all cyclic rotations of sequence x.
The notation yr is used to identify the y sequence in reverse mode, and the set of rows of the matrix Xr is also the set of x sequences in reverse mode.
The notation of the new set is:
Analyzing individually the two sets G(y,x) and Gr (y,x) we can verify that they have identical auto-correlation and cross-correlation properties.
Now, mixing the two sets we obtain a new set:
The set P(y,x) has (4Nc+4) different sequences and the Gold set has only (Nc+2). Then P(y,x) has almost four times more sequences than the Gold set.
An advantage of this set is that you can generate it with few changes in the classical Gold circuit generator:
Figure 1 shows a P(y,x) generator comprising two polynomial generators with octal representations 45 and 67.
Figure 1: This P(y,x) generator comprises two polynomial generators with different octal representations
The purpose of the second clock frequency fc(Nc-1) in Figure 1 is to generate sequences in reverse mode which are "filtered" by a shift register at the end. However, for long sequences, this second frequency fc(Nc-1) would be too high for the operation of the shift registers. A solution is to implement a new circuit, where the m-sequences G1(x) and G2(x) are maintained in a fast read-only memory (ROM) that may be read in ascending or descending order before the last logical "exclusive-or" operation.
The circuit shown in Figure 1 can generate 128 different sequences, while the equivalent circuit for Gold sequences can create only 33. Another characteristic (Figure 2) is that the value of auto-correlation for each sequence is the same.
Figure 2: Periodic auto-correlation for the sequences generated by the circuit of Figure 1.
The maximum value of the absolute peak periodic and aperiodic
cross-correlation is equal to 25; there exists a difference of 19.4% relative to
the peak auto-correlation value (Nc=31). This may be acceptable in some
applications, but it is not high enough for use in wireless communication
systems. For this reason, the next results were obtained with longer segments of
some subsets of Gold-sequences, which may be considered as an alternative for
use in UMTS.
The next simulation was done with segments (38,400 Chips) of a set of Gold
sequences. The primitive polynomial G1(x) is 1+x7+x18 and
the other primitive polynomial G2(x) is 1+x5+x7+x10+x18.
You use these two primitive polynomials to generate scrambling codes for the
UMTS Down Link Channel.
The results of periodic and aperiodic cross-correlation are presented in Tables 1 and 2, respectively. Only the first 512 sequences of the Gold set have been considered in this simulation. The results of the Gold subset are in the shaded cells (column 2) of Tables 1 and 2. These tables do not show the cross-correlation values of the total P(y,x) set, because the m-sequences x, y, xr, and yr are the only four distinct sequences with good correlation properties.
{y
X} with |
{y
X} |
{y
Xr} |
{yr
X} |
{yr
Xr} |
| Maximum Peak | 1202 | 1250 | 1294 | 1426 |
| Average of Max. Peak | 821.05 | 816.67 | 816.83 | 817.32 |
| Average of Min. Peak | -816.05 | -817.30 | -816.82 | -817.18 |
| Minimum Peak | -1226 | -1244 | -1328 | -1292 |
| {yr
X} with |
{y
Xr} |
{yr
X} |
{yr
Xr} |
| Maximum Peak | 1304 | 1204 | 1258 |
| Average of Max. Peak | 817.27 | 817.87 | 816.87 |
| Average of Min. Peak | -816.79 | -812.73 | -817.39 |
| Minimum Peak | -1194 | -1184 | -1230 |
| {y
Xr} with |
{y
Xr} |
{yr
Xr} |
| Maximum Peak | 1246 | 1286 |
| Average of Max. Peak | 817.06 | 817.35 |
| Average of Min. Peak | -812.80 | -817.63 |
| Minimum Peak | -1196 | -1210 |
| {yr
Xr} with |
{yr
Xr} |
| Maximum Peak | 1322 |
| Average of Max. Peak | 821.53 |
| Average of Min. Peak | -815.82 |
| Minimum Peak | -1172 |
Table 1: Periodic cross-correlation of subset P(y,x)
| {y
X} with |
{y
X} |
{y
Xr} |
{yr
X} |
{yr
Xr} |
| Maximum Peak | 1252 | 1248 | 1212 | 1212 |
| Average of Max. Peak | 818.92 | 816.99 | 816.59 | 817.63 |
| Average of Min. Peak | -819.29 | -817.37 | -817.45 | -817.20 |
| Minimum Peak | -1204 | -1250 | -1220 | -1250 |
| {yr
X} with |
{y
Xr} |
{yr
X} |
{yr
Xr} |
| Maximum Peak | 1320 | 1184 | 1270 |
| Average of Max. Peak | 817.20 | 815.13 | 816.83 |
| Average of Min. Peak | -817.57 | -815.09 | -817.26 |
| Minimum Peak | -1222 | -1282 | -1260 |
| {y
Xr} with |
{y
Xr} |
{yr
Xr} |
| Maximum Peak | 1236 | 1194 |
| Average of Max. Peak | 815.65 | 817.05 |
| Average of Min. Peak | -815.44 | -817.50 |
| Minimum Peak | -1210 | -1220 |
| {yr
Xr} with |
{yr
Xr} |
| Maximum Peak | 1262 |
| Average of Max. Peak | 819.14 |
| Average of Min. Peak | -819.12 |
| Minimum Peak | -1244 |
Table 2: Aperiodic cross-correlation of subset P(y,x)
The maximum absolute peak (of periodic and aperiodic cross-correlation) for the Gold subset of 512 different sequences is 1252. Therefore, the difference relative to the auto-correlation value (38,400) is 96.74%, for this subset. The maximum peak (of periodic and aperiodic cross-correlation) for the subset P(y,x) of 2048 different sequences is 1426; the difference relative to the auto-correlation (38,400) is 96.29%. The difference between the Gold subset and the P(y,x) subset, less than 0.5%, is not significant.
Tables 1 and 2 show that the subsets {yr
X} and {y
Xr} are slightly better subsets, with a lower absolute average peak
cross-correlation, as compared with the Gold subset {y
X}.
These results indicate that, by using long sequences of a Gold set, it is possible to increase almost four times the quantity of PN-sequences maintaining a low cross-correlation between all sequences. You can thus use the set P(y,x) in many systems where the maximum quantity of available PN-sequences is primordial for better resource usage.
When you use the complete set P(y,x), it is possible to reduce by four the required chip rate if the degree of the primitive polynomial generators of the Gold set is reduced by two, maintaining the same available quantity of PN-sequences. However, high quality WCDMA systems require the use of high degree polynomial generators.
How Connections are Made
When a UE is set to communicate, it searches for an available cell and requests
a connection. During the cell search, the UE searches for a cell and determines
the downlink scrambling code and common channel frame synchronization of that
cell.
1. Slot Synchronization
In the first step, the UE determines the timing of the cell slot of the primary
synchronization channel (P-SCH) code to synchronize with the targeted cell. The
UE commonly uses a single matched filter to find the P-SCH code by detecting the
peak of the filter response in the received signal.
2. Frame Synchronization
To find the frame synchronization and identify the code group of the scrambling
code, the UE detects the secondary synchronization channel (S-SCH) code in the
received signal and correlates it with all possible secondary synchronization
code sequences. The frame synchronization is determined by the maximum
correlated value.
3. Scrambling Code Identification
The UE determines the primary scrambling code that the targeted cell is using.
It is typically identified using a symbol-by-symbol correlation of the common
pilot channel (CPICH) in the code group that was found in the previous step.
With the primary scrambling code, the UE can detect the primary common control
channel (P-CCPCH) and read the broadcast channel (BCH) information.
The radio frame timing of all common physical channels can be determined after cell search. The P-CCPCH radio frame timing is found during cell search and the radio frame timing of all common physical channels is related to that timing.
P-CCPCH is a fixed rate 30 kbit/s downlink physical channel with a spreading factor of 256 that is used to carry broadcasting information. This channel does not have TPC command and transport format combination information (TFCI). However, it does contain a 256-bit synchronization channel (SCH).
The Random Access Procedure
Once synchronized, the UE can use the random access procedure to initiate a call
through the targeted cell. According to the 3GPP Specification1, the
physical random-access procedure shall be performed as follows:
